TIP
本文主要是介绍 图-代码实现总结 。
# 导航
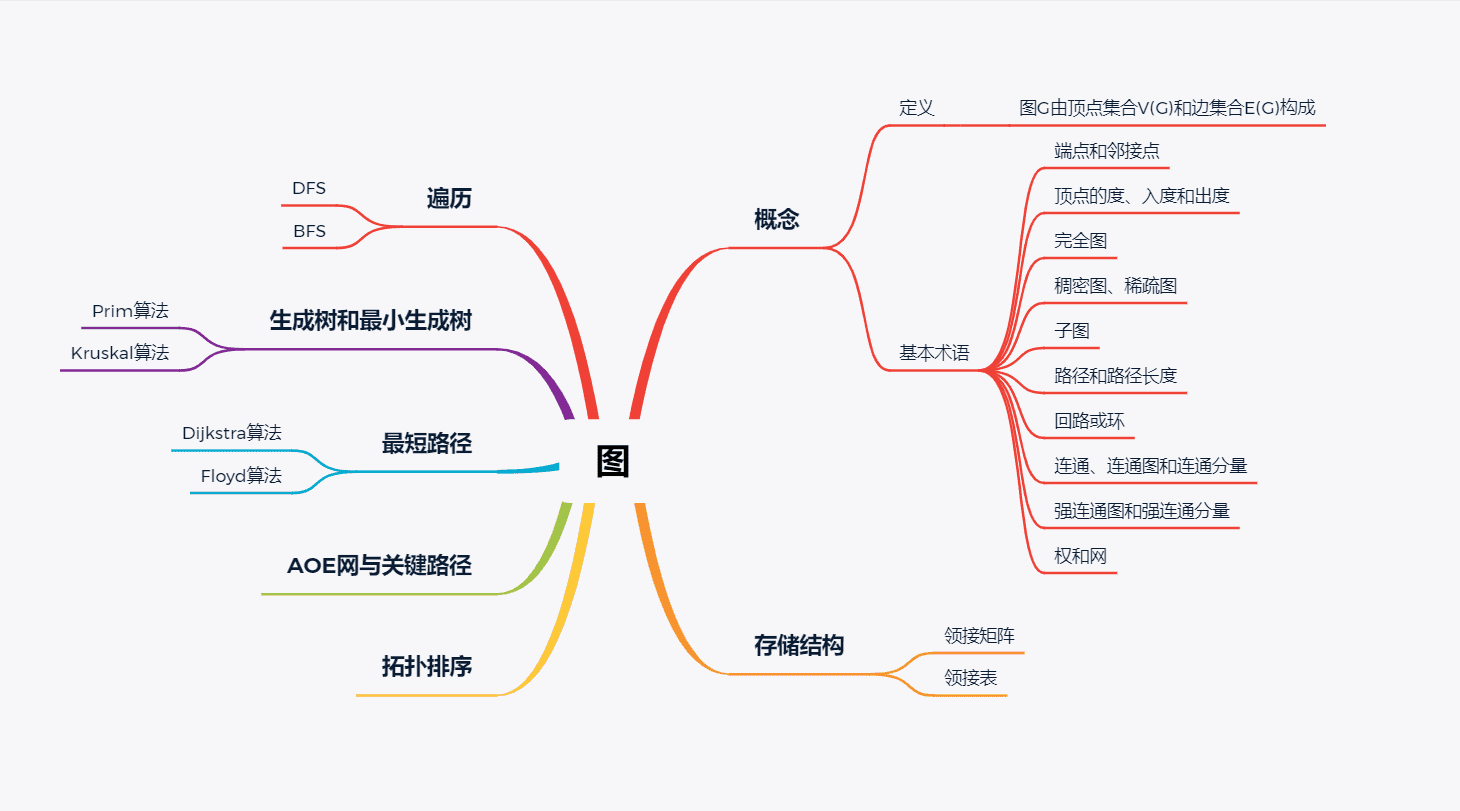
# 二.重要概念*
# 1.DFS 邻接表DFS算法
void DFS(AdjGraph *G,int v)
{ ArcNode *p;
int w;
visited[v]=1; //置已访问标记
printf("%d ",v); //输出被访问顶点的编号
p=G->adjlist[v].firstarc; //p指向顶点v的第一条边的边头结点
while (p!=NULL)
{
w=p->adjvex;
if (visited[w]==0)
DFS(G,w); //若w顶点未访问,递归访问它
p=p->nextarc; //p指向顶点v的下一条边的边头结点
}
}
该算法的时间复杂度为O(n+e)。
采用深度优先遍历方法遍历非连通图
void DFS1(AdjGraph *G)
{ int i;
for (i=0;i<G->n;i++) //遍历所有未访问过的顶点
if (visited[i]==0)
DFS(G,i);
}
非连通图:调用DFS()的次数恰好等于连通分量的个数
# 2.BFS 邻接表BFS算法
void BFS(AdjGraph *G,int v)
{ int w, i;
ArcNode *p;
SqQueue *qu; //定义环形队列指针
InitQueue(qu); //初始化队列
int visited[MAXV]; //定义顶点访问标记数组
for (i=0;i<G->n;i++)
visited[i]=0; //访问标记数组初始化
printf("%2d",v); //输出被访问顶点的编号
visited[v]=1; //置已访问标记
enQueue(qu,v);
while (!QueueEmpty(qu)) //队不空循环
{
deQueue(qu,w); //出队一个顶点w
p=G->adjlist[w].firstarc; //指向w的第一个邻接点
while (p!=NULL) //查找w的所有邻接点
{
if (visited[p->adjvex]==0) //若当前邻接点未被访问
{
printf("%2d",p->adjvex); //访问该邻接点
visited[p->adjvex]=1; //置已访问标记
enQueue(qu,p->adjvex); //该顶点进队
}
p=p->nextarc; //找下一个邻接点
}
}
printf("\n");
}
该算法的时间复杂度为O(n+e)。
采用广度优先遍历方法遍历非连通图
void BFS1(AdjGraph *G)
{ int i;
for (i=0;i<G->n;i++) //遍历所有未访问过的顶点
if (visited[i]==0)
BFS(G,i);
}
非连通图:调用BFS()的次数恰好等于连通分量的个数
# 3.Prim
#define INF 32767 //INF表示∞
void Prim(MatGraph g,int v)
{ int lowcost[MAXV];
int min;
int closest[MAXV], i, j, k;
for (i=0;i<g.n;i++) //给lowcost[]和closest[]置初值
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for (i=1;i<g.n;i++) //输出(n-1)条边
{
min=INF;
for (j=0;j<g.n;j++) //在(V-U)中找出离U最近的顶点k
if (lowcost[j]!=0 && lowcost[j]<min)
{
min=lowcost[j];
k=j; //k记录最近顶点编号
}
printf(" 边(%d,%d)权为:%d\n",closest[k],k,min);
lowcost[k]=0; //标记k已经加入U
for (j=0;j<g.n;j++) //修改数组lowcost和closest
if (lowcost[j]!=0 && g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
Prim()算法中有两重for循环,所以时间复杂度为O(n2)。
Prim算法更适合稠密图求最小生成树。
4.Kruskal
void Kruskal(MatGraph g)
{ int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV];
Edge E[MaxSize]; //存放所有边
k=0; //E数组的下标从0开始计
for (i=0;i<g.n;i++) //由g产生的边集E
for (j=0;j<g.n;j++)
if (g.edges[i][j]!=0 && g.edges[i][j]!=INF)
{
E[k].u=i;
E[k].v=j;
E[k].w=g.edges[i][j];
k++;
}
InsertSort(E,g.e); //用直接插入排序对E数组按权值递增排序
for (i=0;i<g.n;i++) //初始化辅助数组
vset[i]=i;
k=1; //k表示当前构造生成树的第几条边,初值为1
j=0; //E中边的下标,初值为0
while (k<g.n) //生成的边数小于n时循环
{
u1=E[j].u;v1=E[j].v; //取一条边的头尾顶点
sn1=vset[u1];
sn2=vset[v1]; //分别得到两个顶点所属的集合编号
if (sn1!=sn2) //两顶点属于不同的集合
{
printf(" (%d,%d):%d\n",u1,v1,E[j].w);
k++; //生成边数增1
for (i=0;i<g.n;i++) //两个集合统一编号
if (vset[i]==sn2) //集合编号为sn2的改为sn1
vset[i]=sn1;
}
j++; //扫描下一条边
}
}
Kruskal算法的时间复杂度为O(elog2e)。
Kruskal算法更适合稀疏图求最小生成树。
# 5.Dijkstra
void Dijkstra(MatGraph g,int v)
{ int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i<g.n;i++)
{
dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //顶点v到i有边时
else
path[i]=-1; //顶点v到i没边时
}
s[v]=1; //源点v放入S中
for (i=0;i<g.n;i++) //循环n-1次
{
mindis=INF;
for (j=0;j<g.n;j++)
if (s[j]==0 && dist[j]<mindis)
{
u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF && dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
狄克斯特拉算法的时间复杂度为O(n2)。
# 6.Floyd
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{ int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
{
A[i][j]=g.edges[i][j];
if (i!=j && g.edges[i][j]<INF)
path[i][j]=i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j]=-1;
}
for (k=0;k<g.n;k++) //求Ak[i][j]
{
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{
A[i][j]=A[i][k]+A[k][j]; //修改路径长度
path[i][j]=path[k][j]; //修改最短路径为经过顶点k
}
}
}
Floyd算法的时间复杂度为(On3)。
# 7.拓扑排序
拓扑排序步骤
(1)从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它。
(2)从图中删去该顶点,并且删去从该顶点发出的全部有向边。
(3)重复上述两步,直到剩余的图中不再存在没有前驱的顶点为止。
void TopSort(AdjGraph *G) //拓扑排序算法
{ int i,j;
int St[MAXV],top=-1; //栈St的指针为top
ArcNode *p;
for (i=0;i<G->n;i++) //入度置初值0
G->adjlist[i].count=0;
for (i=0;i<G->n;i++) //求所有顶点的入度
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for (i=0;i<G->n;i++) //将入度为0的顶点进栈
if (G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
while (top>-1) //栈不空循环
{
i=St[top];top--; //出栈一个顶点i
printf("%d ",i); //输出该顶点
p=G->adjlist[i].firstarc; //找第一个邻接点
while (p!=NULL) //将顶点i的出边邻接点的入度减1
{
j=p->adjvex;
G->adjlist[j].count--;
if (G->adjlist[j].count==0) //将入度为0的邻接点进栈
{
top++;
St[top]=j;
}
p=p->nextarc; //找下一个邻接点
}
}
}
# 8.AOE网与关键路径
**什么是AOE网
用一个带权有向图(DAG)描述工程的预计进度。
顶点表示事件,有向边表示活动,边e的权c(e)表示完成活动e所需的时间(比如天数)。
图中入度为0的顶点表示工程的开始事件(如开工仪式),出度为0的顶点表示工程结束事件。
什么是关键路径
从AOE网中源点到汇点的最长路径,具有最大长度的路径叫关键路径。
关键路径是由关键活动构成的,关键路径可能不唯一。
*3*|***0***三.疑难问题及解决方案

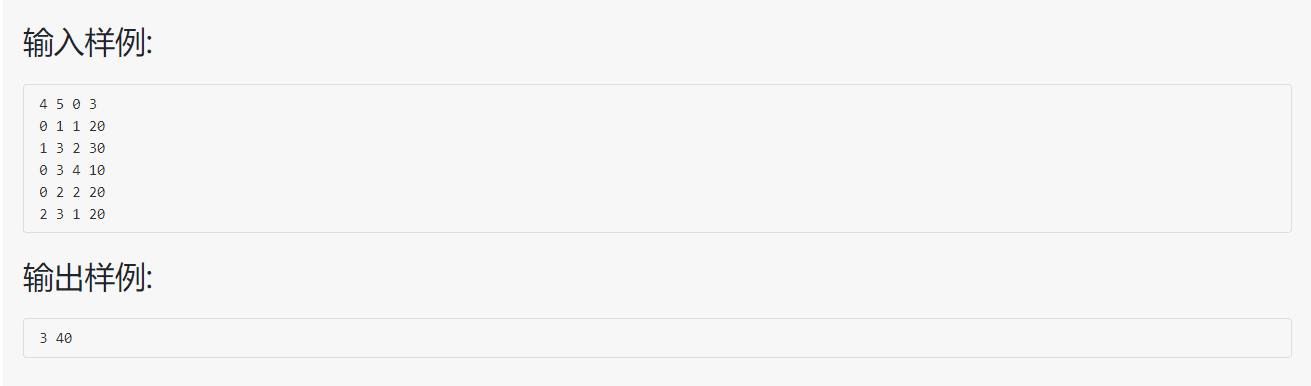
这题考察的是最短路径。
但是有个难点,是相同路径长度,优先考虑过路费最少的那一条。
第一次想法是用两个Dijkstra算法分别求路径和过路费最短,但是有些测试点过不去。
第二次想法是通过Dijkstra算法中的path数组找回路径,但是也只是一条,并不是多条,无法比较过路费。
后面通过百度这个题目,参考别人的代码,将Dijkstra算法进行改进。
void Dijkstra(MyGraph g, int S, int D)
{
int dist[MAXV], path[MAXV], cost[MAXV];
int s[MAXV];
int mindis, i, j, u, star = S;
int sum = 0;
for (i = 0; i < g.vexNum; i++)
{
dist[i] = g.arcs[S][i]; //距离初始化
cost[i] = g.money[S][i];
s[i] = 0; //s[]置空
if (g.arcs[S][i] < INF) //路径初始化
path[i] = S; //顶点v到i有边时
else
path[i] = -1; //顶点v到i没边时
}
s[S] = 1; //源点v放入S中
for (i = 0; i < g.vexNum; i++) //循环n-1次
{
mindis = INF;
for (j = 0; j < g.vexNum; j++)
if (s[j] == 0 && dist[j] < mindis)
{
u = j;
mindis = dist[j];
}
s[u] = 1; //顶点u加入S中
for (j = 0; j < g.vexNum; j++) //修改不在s中的顶点的距离
if (s[j] == 0) {
if (g.arcs[u][j] < INF && dist[u] + g.arcs[u][j] < dist[j])
{
dist[j] = dist[u] + g.arcs[u][j];
path[j] = u;
cost[j] = cost[u] + g.money[u][j];
}
else if (dist[u] + g.arcs[u][j] == dist[j] && cost[u] + g.money[u][j] < cost[j])
{
cost[j] = cost[u] + g.money[u][j];
path[j] = u;
}
}
}
cout << dist[D] << ' ' << cost[D];
}
将路径长度和过路费同时进行Dijkstra算法,但是优先考虑路径长度,长度相同,再比较过路费。
# 参考文章
- https://www.cnblogs.com/yt0617/p/12905732.html











