TIP
本文主要是介绍 图-最短路径(Floyd)算法 。
# 弗洛伊德(Floyd)算法
# 1.定义概览
Floyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
# 2.算法思想
从vi到vj的所有可能存在的路径中,选出一条长度最短的路径。
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。
Floyd算法就是首先只允许经过0号结点,看看是否会变短,如果变短就加之修改,然后只允许经过0,1号结点,看看是否变短,加之修改,直到中间结点到达为所有可能的结点。
# 3.算法过程
定义N阶方阵序列:D−1,D0,D1,D2....D**n−1
D−1[i][j]=G.arc[i][j]
D**k[i][j]=Min{D**k−1[i][j],D**k−1[i][K]+D**k−1[k][j]}
显然: D**k[i][j]是从vi到vj的所经顶点的序号不大于k的最短路径长度。 D**n中为所有顶点偶对vi、vj间的最终最短路径长度。


# 4.画片演示
矩阵坐标从0开始
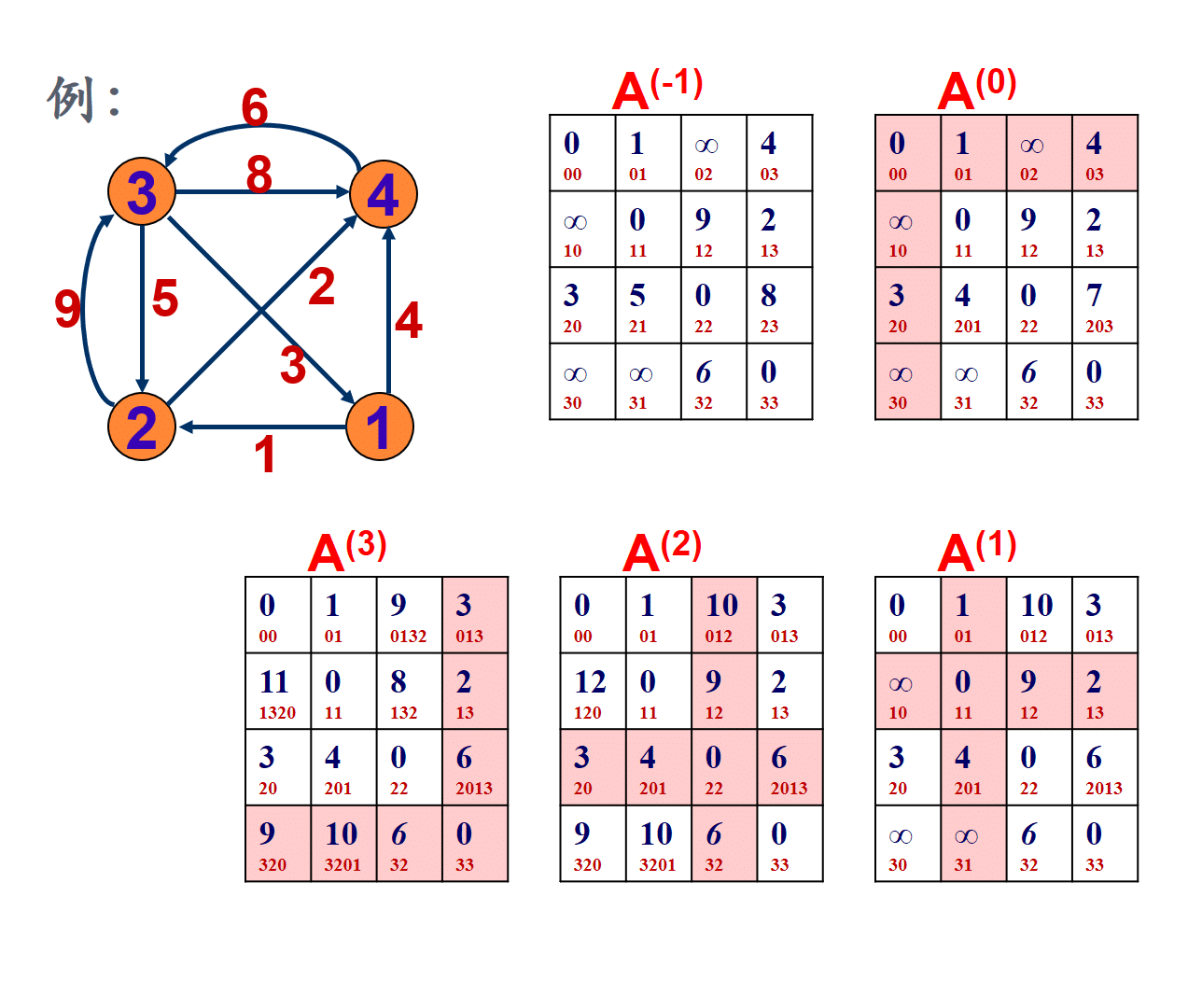
# 5.代码实现
//G-->图,v0-->源点,P[v][w]表示v到其余各点w最短路径,D[v][w]表示v到其余各点w的带权路径长度和
void ShortestPath_Floyd(AdjMatrix *G,int P[MAXVEX][MAXVEX],int D[MAXVEX][MAXVEX]){
int v,w,k;
//初始化D和P
for(v=0;v<G->vexnum;v++){
for(w=0;w<G->vexnum;w++){
D[v][w] = G->acre[v][w];
P[v][w] = w;
}
}
for(k=0;k<G->vexnum;k++){
for(v=0;v<G->vexnum;v++){
for(w=0;w<G->vexnum;w++){
if(D[v][w]>D[v][k]+D[k][w]){ //如果经过下标为k的顶点路径比原两点间的路径更短,则更新
D[v][w] = D[v][k]+ D[k][w];
P[v][w] = P[v][k]; //路径设置经过下标为k的顶点
}
}
}
}
}12345678910111213141516171819202122232425
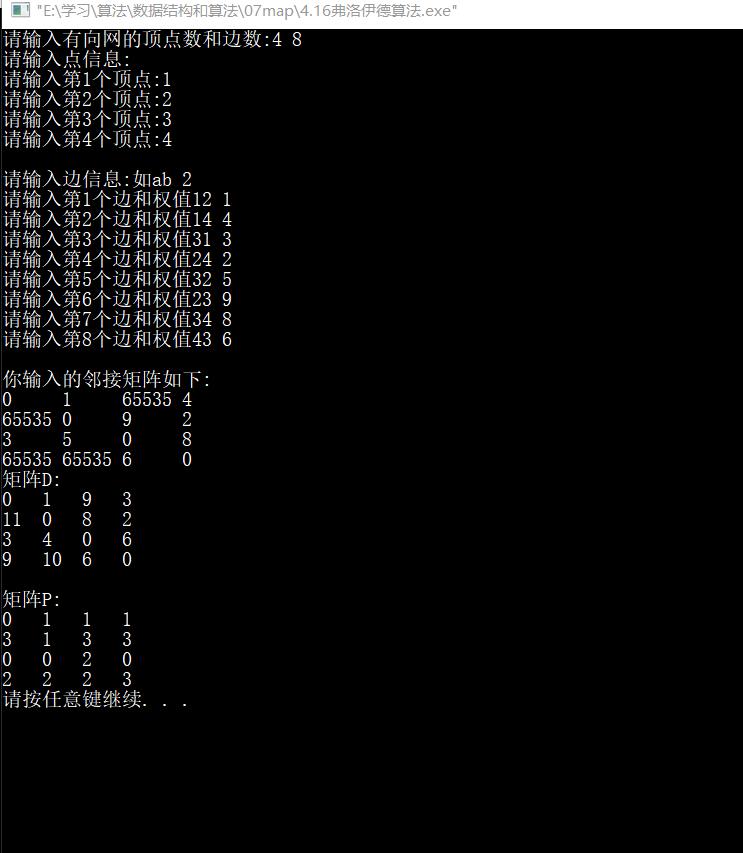
解读路径矩阵P: 已0到3为例:
p[0][3]=1,所以0–>1; p[1][3]=3,所以1–>3; 所以0到3:0–>1–>3
# 源码地址
# 参考资料
《大话数据结构》 《数据结构与算法》
# 参考文章
- https://www.freesion.com/article/1065562680/











