TIP

本文主要是介绍 图-定义和介绍 。

• 图的定义
  • 图定义
  • 图定义和图类型总结：
• 参考文章

图的定义

图定义

图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

（1）在线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图数据元素称之为顶点（Vertex）。

（2）线性表中可以没有数据元素，称之为空表。树中可以没有结点称之为空树。对于图，图中不能没有顶点。强调顶点集合有穷非空。

（3）线性表中，相邻的两点之间具有线性关系，树结构中，相邻两层的结点具有等次关系。而图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示。边集可以是空的。

 **无向边**：若顶点vi到vj之间的边没有方向，则称这条边为**无向边（edge）**，用**无序偶对（vi，vj）**来表示。

 **有向边**：若顶点vi到vj之间的边有方向，则称这条边为有向边，也称为弧**（Arc）**。用有**序偶对<vi,vj>**来表示，**vi称为弧尾（Tail）**，**vj称为弧头（Head）**。如果图中任意两个顶点之间都是有向边，则称该图为**有向图**。

在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。

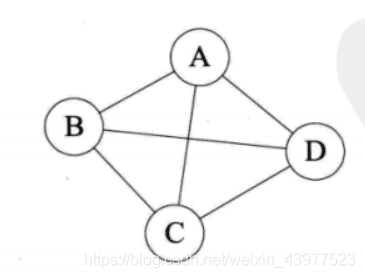
在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。

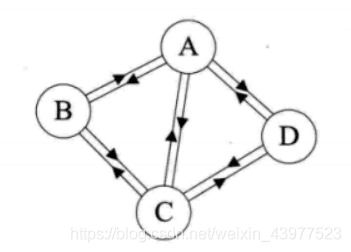
有很少条边的图称为稀疏图，反之称为稠密图。

与图的边或弧相关的数叫作**权（weight），**这种带权的图通常称为网（Network）。

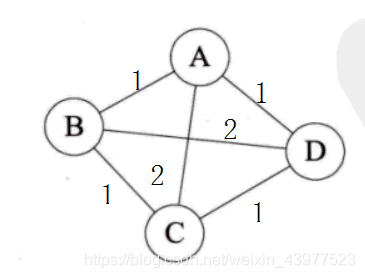
假设有两个图G（V，{E}）和G1=（V1，{E1}），如果V1包含于V，且E1包含于E，则称G1位G的有向图。例子如下：

分别为无向图有其子图，和有向图及其子图。

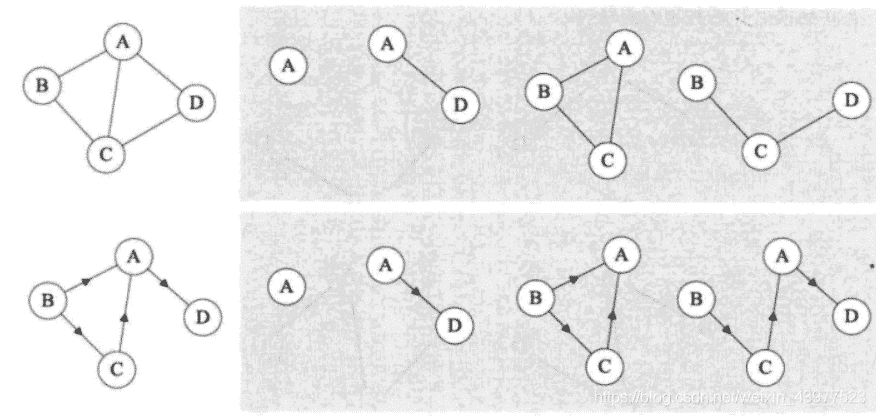
对于无向图G，如果（v，v1）属于E，则称顶点v与v1互为邻接点，即v与v1相邻接

对于有向图G，如果弧<v,v1>属于E，则称顶点v邻接到v1，顶点v1邻接自顶点v。弧<v,v1>与顶点v、v1相关联，以顶点v为头的弧的数目称为v的入度（InDegree），记为ID（v），以v为尾的弧的数目称为v的出度（OutDegree），记为OD（v）；顶点v的度为TD（v）=ID（v）+OD（v）。即顶点的度为此顶点的入度加上出度。

无向图G中从顶点v到顶点v1的路径（Path）是一个·顶点序列

如下图为A到D的四种不同路径：

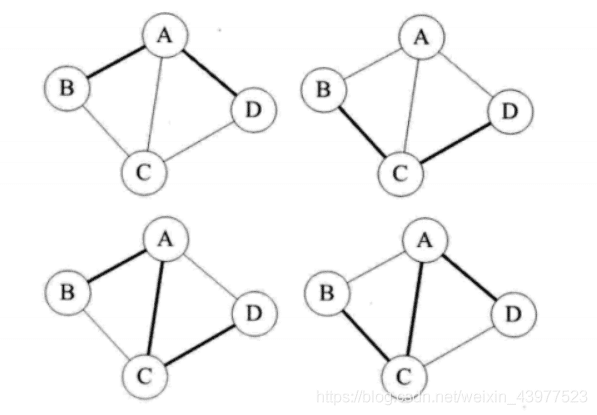
有向图的路径对方向严格要求。

路径的长度是路径上的边或弧的数目。

说的概念有些多，可能脑袋有些晕了吧。我们在来整理下所有的定义与术语。

图定义和图类型总结：

图按照有无方向分为无向图和有向图。无向图由顶点和边构成，有向图由顶点和弧构成。弧有弧头和弧尾之分。

图按照边或弧的多少分为稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。

图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫作度，有向图顶点分为入度和出度。

图上的边或弧上带权则称为网。

图中顶点之间存在路径，两顶点存在路径说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图。有向则称为强连通图。图中有子图，若子图极大连通则就是连通分量，有向的则称为强连通分量。

无向图中连通且n个顶点n-1条边叫生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树，一个有向图由若干棵有向树构成生成森林。

参考文章

• https://blog.csdn.net/weixin_43977523/article/details/89402161